- ASC Proceedings of the 40th Annual Conference
- Brigham Young University - Provo, Utah
- April 8 - 10, 2004
|
Past Performance Information in the Construction Industry
The construction industry has been in a price based, commodity marketplace for the last 30 years. Increasing price pressure has had an impact on performance, levels of risk, and value. The Office of Federal Procurement Policy (OFPP) has encouraged moving to a performance based, best value environment. This environment requires the use of performance information to validate the potential value of a contractor. Extensive testing of the best value process PIPS (Performance Information Procurement System) has shown the information system must minimize the amount of data collection, verification, and management to be sustainable and useable. One of the main issues is that clients are insecure and want to maximize the amount of criteria that identify a contractor’s past performance. Initial tests included more than 40 different performance criteria. It also included different criteria for different types of contractors. The management and maintenance work that resulted made the process unsustainable. This paper analyzes the reduction of criteria to less than ten, and compares the impact on the final results. Using a metric of (1-10), the authors were hypothesizing that a difference of .1 in the prediction of future performance of the contractor would be acceptable. The analysis resulted in a difference of .061. The PIPS process minimized the management and maintenance effort in terms of time and resources by 75% by implementing the minimized performance criteria. There has been no change in the relative performance of the construction contractors using the minimized number of performance criteria.
Keywords: Past Performance, Criteria, Regression, Multicollinearity.
Introduction
The low-bid system has remained the most dominant procurement system. Many users have documented the poor performance and poor quality of contractors that have been procured using the low-bid process (Post, 2001, Angelo, 2001, Hung, 2002). A survey conducted by Engineering News Record showed that 42% of the projects were finished late, 33% were over budget, 13% had pending claims, and only 47% of the owners would never use the same contractors again (Post, 1998). From 1990-1997, over 80,000 contractors failed, leaving behind over $21billion in liabilities (Dun and Bradstreet 1997). European construction nonperformance has had similar results (CIB, 2000, Egan, 1998). Re-engineering, lean construction, partnering, construction management, and supply chain efforts have failed to have a measurable impact on construction performance.
The following are performance issues that arise within the construction industry:
1. Performance of construction will only increase when the contractor is motivated to maximize his or her profit by performing.
2. If past performance is not considered in the hiring of a contractor, the contractor will not be motivated to perform.
3. A contractor’s past performance record is a key indicator for predicting future performance. (Steyaert, 1997).
The U.S. Federal Government establishes past performance information, along with price/cost, as one of the two mandatory evaluation factors in any source selection over a set dollar threshold (Steyaert, 1997b). It is the policy of the Federal Government that agencies use performance-based contracting methods to the maximum extent practicable when acquiring services (Seven Steps, 2002).
Testing Best Value Process Using Past Performance Information
The Performance Based Studies Research Group (PBSRG) at Arizona State University has been testing best-value procurement over the past ten years. The effort included the development of a best-value procurement process named PIPS (Performance Information Procurement System). The characteristics of PIPS include:
1. Use of past performance information on contractors, subcontractors, and key project personnel.
2. Use of the contractor’s ability to identify, prioritize, and minimize risk to measure current capability.
3. Comparison of price and performance without any interpretation of the performance numbers.
4. Use of an information environment to minimize the risk of nonperformance.
Testing commenced in 1994, two years after the creation of the process. Testing started on systems, then incorporated maintenance and repair projects, renovation projects, and new construction. Results were encouraging: 350 tests, $240M of construction, 98% were on time, with no contractor generated cost change orders, and meeting the customer’s expectations of quality and performance (Kashiwagi 2003a).
One of the major differences between the construction industry and other industries is the uniqueness of each construction project. This influenced PBSRG to use the following procedures:
1. Use different criteria for different types of contractors.
2. Use different criteria for different projects.
This resulted in:
1. Repetitive work.
2. Increased workload.
3. Lengthy surveys which past references were resistant to filling out.
4. Confusion in understanding different criteria.
After the experiences at various State organizations, PBSRG decided that the level of management and maintenance of the performance information using a project approach was unsustainable and confusing. This study supports the hypothesis that the number of performance criteria can be minimized and still provides the same result in prioritizing of contractors. This translates into the issue of construction performance being a process issue. Even though all projects are different and require unique performance, the results of a few performance criteria will provide the same value as having the numerous criteria, which take into account project differentials and identify construction performance as a process issue.
Due to the lack of time to analyze the issues, PBSRG had subjectively decided to reduce the criteria to 8. This was a starting point that was going to be iterative if the results were not satisfactory. There were two reasons for using past performance:
1. To ensure that the contractor and key elements had performed in the past.
2. To put the contractor who wins the contract at risk to perform.
The PIPS process does put a contractor, who is awarded the project, at risk through the following mechanisms:
1. The future past performance numbers would be adjusted by 25% of the performance of the current project. By future past performance numbers, the authors’ imply that when contractors finish a project, they are rated on the project, and the ratings affect their past performance rating by 25%. This updated past performance number will be used for future evaluation of the contractor.
2. Due to contractors only turning in their best references, the majority of contractors get the same performance numbers for two of the factors: housekeeping and closeout. However, when an owner concentrates on these two factors, the contractor who wins the contract must ensure that they perform. The best references are submitted because they give the potential value of the contractor’s best personnel. Tests have confirmed that in a true performance based system; the contractor has always sent their best personnel (Kashiwagi 2003b).
Stated differently, past performance numbers are broken up into two different categories. First, they include the numbers that ensure that the contractor has performed in the past. Secondly, it includes numbers that places only the contractor who wins the project at risk.
The analysis resulted in the following:
1. Minimize the number of criteria from 70+ to less than 10 and compare the results from the previous larger set of criteria to a smaller subset of criteria.
2. Compare the smaller subset of criteria obtained from the analysis to the criteria currently being used.
Methodology
All past performance numbers were to come from the best past projects. Contractors were instructed not to submit bad references. True best value procurement forces contractors to submit their best references. They become an accurate predictor of what they will do on a best value procurement. The contractors are forced to decide which are their best references. Every contractor has to do the same thing. Selection of their best projects is the only way to predict future potential. When a contractor gets the job, they have now set a high bar and must continue to perform, or be ejected from the system. The process has multiple screens, the more important being the filters that force the contractor to identify, prioritize and minimize risk (Kashiwagi 2003b).
Regression analysis was used to analyze a data set. The data set contained past performance information (PPI), collected through survey of owners, on actual contractors that participated in the PIPS process (173 contractors). The data set used general contractors PPI, electrical contractors PPI, and fire alarm contractors PPI. Table 1 summarizes the analysis approach. The details of the analysis can be found in the Appendix.
Table 1
Summary of analysis approach
|
Step 1 : Data Splitting |
|
|
|
Data was divided into 70% estimation data and 30% testing data. Thus there were approximately 123 records in estimation data and 50 records in testing data. The steps that follow were carried out on the estimation data. |
|
Step 2 : Multicollinearity diagnostics were performed. |
|
|
|
Variance Inflation Factors (VIFs) were examined for all variables. |
|
|
Once multicollinearity was confirmed,
eigensystem analysis of correlation matrix ( |
|
Step 3 : Multicollinearity was dealt using following method. |
|
|
|
Principal Component Regression (using Minitab software) |
|
Step 4 : Variable importance was determined. |
|
|
|
Based on principal component regression & domain knowledge, reduction in survey questionnaire was achieved and then new models in terms of original variables were fit using all possible regression. |
|
Step 5 : Evaluation of Candidate models using all subset regression. |
|
|
|
Candidate models were evaluated using different criteria such as Cp, MSE, Adjusted R-square, Predicted R-square. |
|
Step 6 : Model adequacy checks were performed for the final model |
|
|
|
Residuals versus fitted values plot for checking constant variance assumption. |
|
|
Normal probability plot of residuals for checking normality assumption. |
|
Step 7: Testing data was used to validate the final model. |
|
|
Step 8: The subset criteria obtained were compared with the current criteria |
|
The analysis suggests that use of a standardized set and a smaller subset of criteria can produce results that are comparable to results obtained from using a much larger set of unstandardized (changes with the trade) criteria.
Comparison Of New Subset With The Current Subset
Table 2 below shows the current subset of criteria used by PBSRG for their survey questionnaire
Table 2
Criteria appearing in current survey questionnaire
|
Criteria Number |
Description |
|
1 |
Ability to manage the project cost (minimize change orders) |
|
2 |
Ability to maintain project schedule (complete on-time or early) |
|
3 |
Quality of workmanship |
|
4 |
Professionalism and ability to manage (includes responses and prompt payment to suppliers and subcontractors) |
|
5 |
Close out process (no punch list upon turnover, warranties, as-builts, operating manuals, tax clearance, etc. submitted promptly) |
|
6 |
Communication, explanation of risk, and documentation (construction interface completed on time) |
|
7 |
Ability to follow the user rules, regulations, and requirements (housekeeping, safety, OSHA, etc…) |
|
8 |
Overall customer satisfaction (comfort level in hiring contractor again) |
Table 3 below summarizes the subset criteria obtained from the analysis.
Table 3
Subset criteria obtained from analysis
|
Criteria Number |
Description |
|
1 – X30 |
Comfort level in hiring contractor again based solely on performance |
|
2 – X28 |
Overall performance of the contractor |
|
3 – X25 |
Overall skill of the craftsmen |
|
4 – X24 |
Professionalism of the contractor |
|
5 – X22 |
OSHA / EPA / DOL knowledge and compliance |
|
6 – X19 |
Contractor’s management abilities |
|
7 – X16 |
Contractor’s flexibility in handling unforeseen events |
|
8 – X17 |
Contractor’s housekeeping |
|
9 – X15 |
Compliance with owner’s safety programs |
|
10 – X14 |
Efficiency of on-site communication |
The analysis agrees with six of the eight criteria appearing in the current survey questionnaire. The criterion that appears in the new subset, which are not currently being asked, are included for the evaluation of a contractor on a current best-value project. There is one criterion appearing in the current survey, which is not appearing as important from the analysis. It can be evaluated based on domain knowledge and removed from the current questionnaire.
Conclusion
This study supports the hypothesis that fewer criteria can result in a more sustainable, efficient, and successful best-value process. It also validates PBSRG’s efforts in reducing the number of criteria from over 70, to less than 10. Use of regression analysis gives an equation, which can be used to predict a contractor’s future performance (in terms of the overall satisfaction which an owner might get by hiring that contractor). The results of this paper can be expected only in conjunction with the proper use of the PIPS environment.
References
Angelo, W. (2001, June 25). Web Voters Seek Alternatives. Engineering News Record (ENR), 246 [25], pg. 107.
CIB. (2000). The State of the Construction Industry Report, (2000). Construction Industry Board. [11]. URL:http://www.dti.gov.uk/construction/stats/soi/soi11.htm.
Dun and Bradstreet. (1997). Dun & Bradstreet Business Failure Record, 1990-1997. Surety Information Office (SIO). Date accessed (12/29/2003) URL: http://www.sio.org/HTML/whyfail.html/.
Egan, Sir John. (1998, July 16). Rethinking Construction: The Report of the Construction Task Force to the Deputy Prime Minister, John Prescott, on the scope for improving the quality and efficiency of UK construction. The Department of Trade and Industry (dti). URL: http://www.dti.gov.uk/construction/rethink/report/index.htm.
Hung, T. (2002, May). Prequalification and Qualified Tendering Group: A Perspective From the Hong Kong Ground Investigation Industry. Cost Engineering, 44 [5], pgs. 36-42.
Kashiwagi, Dean and J. Savicky. (2003a). “Case Study of the Implementation of the Performance Information Procurement System at the Dallas Independent School District.” Associated Schools of Construction (ASC) International Proceedings of the 39th Annual Conference, Clemson, SC, pgs. 315-323.
Kashiwagi, Dean T., Darshit Parmar, and John Savicky. (September 2003b). The Impact of Minimising Specifications & Management at the University of Hawaii. Journal of Facilities Management 2003. 2 [2], pgs. 131-141.
Montgomery, Peck, Vining. Introduction to Linear Regression Analysis, (3rd ed.).
Post, N. (1998, May 11). Building Teams Get High Marks. Engineering News Record (ENR), 240 [19], pgs. 32-39.
Post, N. (2001, May 14). Bumpier Road to Finish Line. Engineering News Record (ENR), 246 [19], pgs. 56-63.
Seven Steps to Performance-Based Services. (2002, January). Acquisition Benchmark Version. OAMWeb. URL http://oamweb.osec.doc.gov/pbsc/home.html.
Steyaert, J. (1997, December). White paper past performance. U.S. General Services Administration. Date accessed (5/16/2002). URL: http://www.acqsolinc.com/pastperfdoc/pastperfwp.html.
Steyaert, J. (1997b, December). White paper past performance, OFPP Letter No. 92-5. U.S. General Services Administration. Date accessed (5/16/2002). URL: http://www.acqsolinc.com/pastperfdoc/pastperfwp.html.
Appendix
The authors suspected the presence of multicollinearity based on the domain knowledge and the data set. For example, if the contractor is a high performer, then one would expect that the contractor will receive high ratings for variables like “overall performance of the contractor” and “contractor’s management abilities”. Multicollinearity diagnostic was done to verify the presence of multicollnearity.
A correlation matrix (![]() ) was constructed on the standardized data and the
off-diagonal elements were examined. Inspection revealed the presence of several
near-linear dependencies in the data set. To further confirm our
multicollinearity diagnosis and to determine the extent of multicollinearity,
the authors examined the variance inflation factors and performed a eigensystem
analysis.
) was constructed on the standardized data and the
off-diagonal elements were examined. Inspection revealed the presence of several
near-linear dependencies in the data set. To further confirm our
multicollinearity diagnosis and to determine the extent of multicollinearity,
the authors examined the variance inflation factors and performed a eigensystem
analysis.
There were 19 variables whose VIF was greater than 10 and the largest VIF was 26.3. Looking at the VIFs and keeping in mind the fact that these VIFs are based on standardized data, it was concluded that severe multicollinearity exists in the data set. The eigenvalues and corresponding eigenvectors of the correlation matrix were determined using Minitab. Condition indices were then determined. Two condition indices exceeded 1000 and 20 others exceeded 100. The authors therefore concluded presence of at least two strong near-linear dependencies in the data set.
Thus, based on examination of correlation matrix, VIFs and condition indices, the authors were able to conclude the presence of multicollinearity and were also able to measure the extent of multicollinearity.
Multicollinearity was dealt with using principal component regression (PCR). Before doing regression on principal components, the authors had to decide on the number of components to retain. This was done using the scree plot as shown in Figure 1 below.
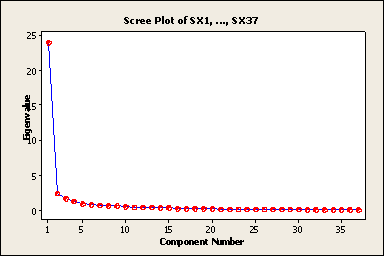
Figure 1: Scree Plot
The authors examined differences between models by doing an all subset regression using five components. Performing a regression with Y (Customer satisfaction) in the standardized form as the response results in the information obtained from Minitab shown below.
Best Subsets Regression: Std Y versus Z1, Z2, Z3, Z4, Z5
Response is Std Y (Standardized Values of Customer Satisfaction) in table below.
|
Vars |
R-Sq |
R-Sq(adj) |
Mallows C -p |
S |
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
|
1 |
87.1 |
87.0 |
0.8 |
0.032621 |
X |
|
|
|
|
|
1 |
0.2 |
0.0 |
809.3 |
0.090812 |
|
|
|
X |
|
|
2 |
87.3 |
87.1 |
0.7 |
0.032475 |
X |
|
|
X |
|
|
2 |
87.2 |
87.0 |
2.3 |
0.032695 |
X |
|
X |
|
|
|
3 |
87.4 |
87.1 |
2.3 |
0.032548 |
X |
|
X |
X |
|
|
3 |
87.4 |
87.0 |
2.5 |
0.032582 |
X |
X |
|
X |
|
|
4 |
87.4 |
87.0 |
4.1 |
0.032656 |
X |
X |
X |
X |
|
|
4 |
87.4 |
87.0 |
4.2 |
0.032676 |
X |
|
X |
X |
X |
|
5 |
87.4 |
86.9 |
6.0 |
0.032786 |
X |
X |
X |
X |
X |
The authors selected the model with Z1 and Z4 based on smaller C-p, higher Adjusted R-square and smaller S, then fit a regression model with Z1 and Z4. The results obtained from Minitab are as shown below.
Regression Analysis: Std Y versus Z1, Z4
The regression equation is
Std Y = - 0.00000 + 0.0173 Z1 + 0.00384 Z4
|
Predictor |
Coef |
SE Coef |
T |
P |
VIF |
|
Constant |
-0.000004 |
0.002928 |
-0.00 |
0.999 |
|
|
Z1 |
0.0172629 |
0.0006006 |
28.74 |
0.000 |
1.0 |
|
Z4 |
0.003836 |
0.002650 |
1.45 |
0.150 |
1.0 |
S = 0.0324747 R-Sq = 87.3% R-Sq(adj) = 87.1%
PRESS = 0.140334 R-Sq(pred) = 85.97%
Analysis of Variance
|
Source |
DF |
SS |
MS |
F |
P |
|
Regression |
2 |
0.87352 |
0.43676 |
414.14 |
0.000 |
|
Residual Error |
120 |
0.12655 |
0.00105 |
|
|
|
Total |
122 |
1.00007 |
|
|
|
Converting this model in terms of original variables to look at the coefficients of the original variables, the authors used the results obtained from principal component regression and the domain knowledge to summarize the preliminary subset of criteria. These are as shown in Table 4 below.
Table 4
Preliminary Subset variables selected
|
Subset Variable |
Description |
|
X30 |
Comfort level in hiring contractor again based solely on performance |
|
X27 |
Overall construction quality |
|
X21 |
Quality of workmanship |
|
X23 |
Contractor’s level of honesty |
|
X28 |
Overall performance of contractor |
|
X22 |
OSHA / EPA / DOL knowledge and compliance |
|
X25 |
Overall skill of craftsman |
|
X24 |
Professionalism of contractor |
|
X19 |
Contractor’s management abilities |
|
X26 |
Overall construction knowledge |
|
X16 |
Contractor’s flexibility in handling unforeseen events |
|
X17 |
Contractor’s housekeeping |
|
X15 |
Compliance with owner’s safety programs |
|
X29 |
Customer public relations |
|
X8 |
Ability to minimize change orders |
|
X13 |
Ability to produce required permits / documentation |
|
X14 |
Efficiency of onsite communication |
The above subset of criteria can be used to evaluate the candidate models using all subset regression technique. The results obtained from Minitab are shown below.
|
|
|
|
|
|
|
x |
x |
x |
x |
x |
x |
x |
x |
x |
x |
x |
x |
x |
x |
|
x |
x |
|
|
|
|
|
|
|
3 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
2 |
1 |
1 |
1 |
2 |
x |
1 |
1 |
|
Vars |
R-Sq |
R-Sq (adj) |
Mallows C-p |
S |
|
0 |
7 |
1 |
3 |
8 |
2 |
5 |
4 |
9 |
6 |
6 |
7 |
5 |
9 |
8 |
3 |
4 |
|
1 |
85.4 |
85.3 |
119.6 |
0.15228 |
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
84.1 |
84 |
141.2 |
0.15904 |
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
89.6 |
89.5 |
52.9 |
0.12906 |
|
X |
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
89.3 |
89.1 |
58.1 |
0.13102 |
|
X |
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
3 |
91 |
90.8 |
32 |
0.12052 |
|
X |
|
|
|
|
|
X |
|
|
|
|
|
X |
|
|
|
|
|
3 |
91 |
90.8 |
32.8 |
0.12084 |
|
X |
|
|
|
X |
|
|
|
|
|
|
|
X |
|
|
|
|
|
4 |
91.6 |
91.3 |
24.3 |
0.11699 |
|
X |
|
|
|
X |
|
X |
|
|
|
|
|
X |
|
|
|
|
|
4 |
91.6 |
91.3 |
24.5 |
0.11705 |
|
X |
|
|
|
|
|
X |
|
|
|
|
|
X |
|
|
|
X |
|
5 |
92.1 |
91.8 |
18.2 |
0.11395 |
|
X |
|
|
|
|
|
X |
X |
|
|
|
|
X |
|
|
|
X |
|
5 |
92.1 |
91.7 |
19 |
0.11433 |
|
X |
|
|
|
|
|
X |
X |
|
|
X |
|
X |
|
|
|
|
|
6 |
92.6 |
92.2 |
12 |
0.11077 |
|
X |
|
|
|
X |
|
X |
X |
|
|
|
|
X |
|
|
|
X |
|
6 |
92.6 |
92.2 |
12.7 |
0.11108 |
|
X |
|
|
|
|
|
X |
X |
|
|
X |
|
X |
|
|
|
X |
|
7 |
92.9 |
92.5 |
9.3 |
0.10904 |
|
X |
|
|
|
X |
|
X |
X |
|
|
X |
|
X |
|
|
|
X |
|
7 |
92.8 |
92.3 |
11.8 |
0.11023 |
|
X |
|
|
|
X |
|
X |
X |
X |
|
|
|
X |
|
|
|
X |
|
8 |
93.1 |
92.6 |
8.1 |
0.10804 |
|
X |
|
|
|
X |
|
X |
X |
X |
|
X |
|
X |
|
|
|
X |
|
8 |
93.1 |
92.6 |
8.3 |
0.10813 |
|
X |
|
|
|
X |
|
X |
X |
|
X |
X |
|
X |
|
|
|
X |
|
9 |
93.2 |
92.6 |
8.8 |
0.10786 |
|
X |
|
|
|
X |
X |
X |
X |
X |
|
X |
|
X |
|
|
|
X |
|
9 |
93.2 |
92.6 |
8.9 |
0.10794 |
|
X |
|
|
|
X |
X |
X |
X |
|
X |
X |
|
X |
|
|
|
X |
|
10 |
93.3 |
92.7 |
8.1 |
0.10704 |
|
X |
|
|
|
X |
X |
X |
X |
X |
|
X |
X |
X |
|
|
|
X |
|
10 |
93.3 |
92.7 |
8.5 |
0.10723 |
|
X |
|
|
|
X |
X |
X |
X |
|
X |
X |
X |
X |
|
|
|
X |
|
11 |
93.4 |
92.8 |
8.7 |
0.10681 |
|
X |
|
|
|
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
X |
|
11 |
93.4 |
92.8 |
9.1 |
0.10702 |
|
X |
X |
|
|
X |
X |
X |
X |
|
X |
X |
X |
X |
|
|
|
X |
|
12 |
93.5 |
92.8 |
9.3 |
0.1066 |
|
X |
X |
|
|
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
X |
|
12 |
93.4 |
92.7 |
10.4 |
0.10718 |
|
X |
|
|
|
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
X |
|
13 |
93.5 |
92.8 |
10.8 |
0.10685 |
|
X |
X |
|
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
X |
|
13 |
93.5 |
92.8 |
11.1 |
0.10699 |
|
X |
X |
|
|
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
X |
X |
|
14 |
93.6 |
92.7 |
12.6 |
0.10722 |
|
X |
X |
|
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
X |
|
14 |
93.6 |
92.7 |
12.6 |
0.10722 |
|
X |
X |
|
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
X |
X |
|
15 |
93.6 |
92.7 |
14.3 |
0.10757 |
|
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
X |
|
15 |
93.6 |
92.7 |
14.4 |
0.10763 |
|
X |
X |
|
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
X |
X |
|
16 |
93.6 |
92.6 |
16.2 |
0.10801 |
|
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
X |
X |
|
16 |
93.6 |
92.6 |
16.2 |
0.10803 |
|
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
X |
|
17 |
93.6 |
92.6 |
18 |
0.10845 |
|
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
Th authors evaluated the above candidate models obtained from all subset regression technique using C-p, adjusted R-sq, MSE and also by looking at the VIFs. The model (highlighted above) with ten variables had minimum C-p, high-adjusted R-sq and low MSE. This model was selected and then was subjected to the model adequacy checks.
Model Adequacy Checks
A couple of points were turning out to be outliers. Further examination of these points suggested data recording errors. They were hence removed from the data set. A model was fit again for the selected variables. Examination of normal probability plot and residuals versus fitted values plot did not give any indication of normality and constant variance assumptions violation. The model obtained is as under:
The regression equation is
Response = 0.508 + 0.341 X30 + 0.269 X28 - 0.0584 X22 + 0.171 X25 - 0.0450 X24 - 0.0242 X19 + 0.0473 X16 + 0.0015 X17 + 0.102 X14 + 0.143 X15
|
Predictor |
Coef |
SE Coef |
T |
P |
VIF |
|
Constant |
0.5076 |
0.2703 |
1.88 |
0.063 |
|
|
X30 |
0.34085 |
0.05467 |
6.24 |
0.000 |
7.0 |
|
X28 |
0.26913 |
0.07640 |
3.52 |
0.001 |
11.8 |
|
X22 |
-0.05843 |
0.04994 |
-1.17 |
0.245 |
6.6 |
|
X25 |
0.17083 |
0.05243 |
3.26 |
0.001 |
6.0 |
|
X24 |
-0.04497 |
0.07545 |
-0.60 |
0.552 |
8.2 |
|
X19 |
-0.02421 |
0.06084 |
-0.40 |
0.691 |
7.9 |
|
X16 |
0.04726 |
0.03917 |
1.21 |
0.230 |
4.3 |
|
X17 |
0.00149 |
0.04566 |
0.03 |
0.974 |
5.5 |
|
X14 |
0.10231 |
0.05365 |
1.91 |
0.059 |
6.0 |
|
X15 |
0.14312 |
0.06100 |
2.35 |
0.021 |
6.7 |
S = 0.0944937 R-Sq = 94.0% R-Sq(adj) = 93.4%
PRESS = 1.30484 R-Sq(pred) = 91.98%
Analysis of Variance
|
Source |
DF |
SS |
MS |
F |
P |
|
Regression |
10 |
15.2833 |
1.5283 |
171.16 |
0.000 |
|
Residual Error |
110 |
0.9822 |
0.0089 |
|
|
|
Total |
120 |
16.2655 |
|
|
|
Above results indicated that the VIFs were now under control for all variables except X28. Considering the nature of problem on hand and the fact that the model is fit in terms of original variables, the slightly higher VIF in X28 variable does not appear to be of any grave concern. The model seemed to be having a good predictive power with a predicted R-square of 91.98 %. To further validate our model, testing data was used which was kept aside earlier.
Model Validation Using Testing Data
50 randomly selected records (contractors) from the original sample of 173 were used for model validation. The average squared prediction error was calculated using the following equation.
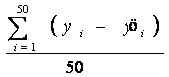
The average squared prediction error of the new sample was 0.087 (50 new contractors). This error rate is larger than the residual mean square of the estimation data, which was 0.009 (based on the estimation data set). However, it is acceptable considering the nature of the problem in hand.
Further model validation was performed using data from different types of contractors. 29 contractors were analyzed from HVAC, painting, and plumbing. The average squared prediction error using the three new types of contractors was 0.016. Table 5 illustrates the analysis of all of the tests. The combined average of all the trades showed an overall average of 0.06
Table 5
Average squared prediction error for testing data
|
Type of Contractor |
Number used in Testing |
Average Squared Prediction error |
|
General |
26 |
0.088 |
|
Electrical |
14 |
0.142 |
|
Fire Alarm |
10 |
0.009 |
|
HVAC |
9 |
0.022 |
|
Painting |
10 |
0.006 |
|
Plumbing |
10 |
0.022 |
|
Overall Average |
0.061 |
|
Model Validation Using Testing Data
This analysis suggests that use of standardized set and a smaller subset of criteria can produce results that are comparable to results obtained from using a much larger set of unstandardized (changes with the trade) criteria.