Matrix Effectiveness Review Technique (MERT), A Tool For Construction Management

(pressing HOME will start a new search)

ASC Proceedings of the 28th Annual Conference
Brigham Young University-Provo, Utah
April 18-20, 1991 pp 83-86

MATRIX EFFECTIVENESS REVIEW TECHNIQUE (MERT) A TOOL FOR CONSTRUCTION MANAGEMENT

Paul Bunea
Fairleigh Dickinson University
Teaneck, New Jearsey

A matrix in construction management could be defined as a set of objectives to be regularly reviewed, monthly, bi-monthly, or quarterly for the purpose of setting priorities, reevaluation, and progress performance, by interfacing the Owner/ Entrepreneur's (0/E) objectives with the organizations which produce the stages of planning, design, execution of quality construction, namely Architects/Engineers (A/E), Construction Managers (CM), General Contractors (GC), or even large basic Subcontractors (Sub) or Primes.

Objective setting could be a procedure of ratings on a scale from 1 to 5, whereby 1 = excellent or 100'%. effective and 5 = failure or completely unacceptable performance for each time-set period, as it may be.

These matrixes can be calculated either by the O/E or the CM. In either case. the approach to the rating system must be absolutely unbiased, reflecting entirely the occured facts. Perhaps the calculation should be done by both parties and an average between the two could be a fair evai,aati on.

As a point of reference, a meeting of the minds between O/E and CM should produce an agreed ideal number for each period, which in cumulative sommation for all periods will reach a total ideal number representing in advance, before the project starts, the thriving goal. Any resulting number equal or slightly lower, will demonstrate the effectiveness of the whole integrated project performance. If the cumulative point sommation over the time periods is much higher compared to the ideal, the project has gone off the track,it derailed, it soured, it became tardy, and its cost or expenses were much higher than estimated.

If this ideal number or any variations thereof up or down, within reasonable limits, can be made integral part of a GMC

(Guaranteed Maximum Cost) contract agreement between O/E and CM, besides the CM's agency, barring or disclaiming any extraordinary larqe or affecting change-orders, the unrehearsed performance of all phases of a construction project could eventually become a contractual quasi-guaranteed task.. RATING SYSTEM

The system of interfacing O/E's project objectives with ;CM-A/E's building performance is rated from _1 to 5 for each interfaced or independent activity in a matrix: 1 meaning perfection and 5 meaning failure. Since construction is a sequential series of unrehearsed activities, a rating of 1, meaning absolute perfection is unlikely and improbable, thus, the following scale of ratings for each interfaced objective versus building performance could be summarized as follows:

1.0........ per-Feat performance (improbable) 1.5........ good performance

2.0........ acceptable performance 2.5........ acceptably mediocre performance 3.0........ viably poor performance 3.5........ viably very poor performance 4.0........ unacceptable performance 4.5........ managerially failed performance 5.0........ disastrous performance necessitating substitution of

managerial skills

In-between interpolations could be very acceptable.

ALGORITHMIC MATRIXES

These matrixes are represented by algebraic determinants. Barring any onerous calculations, the 3 :: 71 determinant matrix is sufficient for lay people, given the easy algorithm of solution reproduced herein. A 4 x 4 determinant matrix would be a tremendous refinement in "long-hand". Once the needed refinement is over 4 x -4, a

mathematical computer software tool becomes a real necessity.

To translate the whole matter into simple mathematical language, coe could state that if the CPM or PERT schedule meganetwork shows a completion time for a construction project in "n" time periods, a cumulative matrix determinant value of

will evaluate the efficiancy and effectiveness at the end of each time period, until "Mn" would represent total cumulative matrix value upon completion, or the number set by O/E and CM.

A :a determinant matrix can be represented thus:

The numbers after each element represent the row and the column respectively.

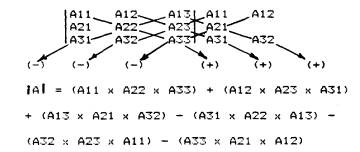
To resolve numerically the 3 x 1 determinant matrix, the following easy algorithm may be used:

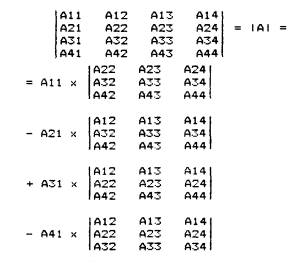
When the determinant matrix is a 4 x 4, it may be reduced to a 3 x ? or various 2 x _2. For that, one must brush-up on elementary Algebra. Following equations depict the solution of a 4 x 4 determinant:

ILLUSTRATIVE EXAMPLE

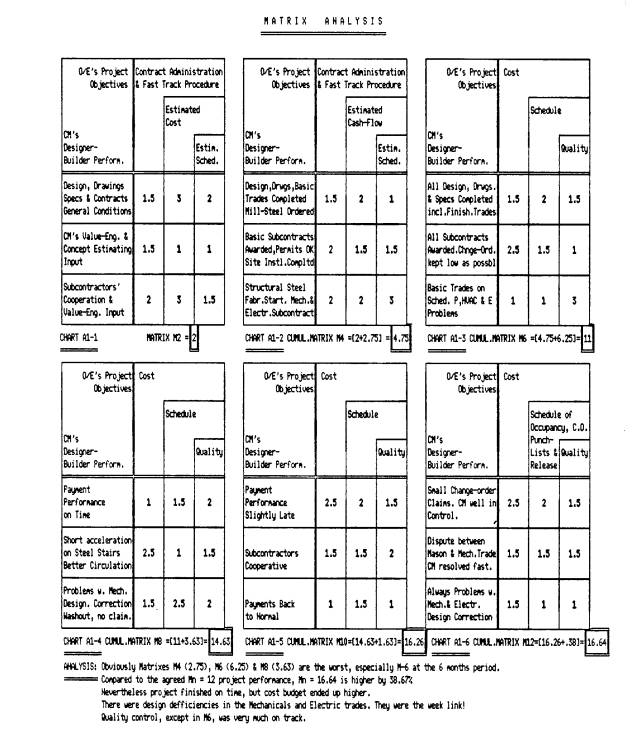
Let us take the following example on a 2month evaluation frequency period for each matrix determinant. The project is to last 12 months or 6 periods; first 2 periods are planning stages and last 4 are construction stages at jobsite.

The ideal reasonable "negotiated" cumulative number to thrive for agreed between O/E and CM is Mn = 12 upon completion.

In case of a larger job, lasting 2 years for example, if the evaluation frequency period for each matrix determinant is taken on a monthly basis, the reasonable negotiated cumulative number could be between a minimum of 24 x 1.75 = 42 or a maximum of 24 x 2 = 48. Any final result upon completion between 42 and 48, would complement a GMC as a definite guarantee to the O/E by the CM.

IMPORTANT COMPUTATION RULES

(1) If all rating numbers in a matrixdeterminant are the same, the determinant = O, which is absurd and impossible regardless of any applied rating, since "O" would enhance the cumulative final rating fictitiously and ineffectively, which could be considered as "cheating" the process.

(2) Ignore any negative (-) result of any partial determinants in the cumulative process; assume all determinants to be positive (+) in their cumulative periodic sommation.

(3) The final cumulative ideal rating number must be:

(a) function of the project duration; (b) frequency function of matrix computation for any repetitive time period;

(c) a mutual agreement as to final rating-goal-number between O/E and CM-A/E (both O/E's agents, even when CM is also designerbuilder CD/B/CM7, not or at risk without or with a GMC);

(d) a rating-goal-number under contractual obligation, especially if a GMC at risk is involved.

PRACTICAL CONCLUSION

Besides the "at risk" GMC, the above could be used as a marketing tool by the CM, to "sweeten" the contractual fee agreement upwards by perhaps another percentage point.

ACKNOWLEDGEMENTS

For computations of more than 2 x determinants, we recommend the use of MATRIX MASTER, Clark Kimberling Mathematics Software Co.,419 S. Boeke Rd., Evansville, IN 47714, (912^)479-6665. It can solve determinants up to 30 x 30.

REFERENCES

Project Management, A Managerial Approach: -nd Ed. by J. Meredith & S. J. Mantel Jr. J. Wiley & Sons, Publ.

Economics of Building: R. Johnson, J. Wiley S Sons, Publ.