Using Spreadsheets to Optimally Unbalance a Construction Bid

Introduction

Many contractors have spreadsheet program on their computer and their use in construction cost estimating, cost analysis and control is increasing (Carmichael 1997). While the possibilities for automating and customizing spreadsheets are unlimited, they are mostly used to set up basic cost breakdown summary sheets with basic formulas (Christofferson 2000). Christofferson (1999) presented some helpful methods that convert basic spreadsheets into useful tools to accomplish estimates quickly and accurately including setting up a summary sheet, creating detail sheets, information lookup methods for estimating and, data validation. This paper presents another useful use of spreadsheets to optimally unbalance the unit prices on a construction bid. The proposed spreadsheet application can be used by contractors in real life situations to help in unbalancing their bids to maximize profits, as well as in a classroom setting to teach construction students about the effects of bid unbalancing on the profit. The remainder of this paper is organized as follows: bid unbalancing is discussed in the next section. This is followed by a description of the proposed spreadsheet model. The use of the spreadsheet model is demonstrated through a simple example and the results are discussed. Finally, the conclusions and recommendations for future developments are presented.

Bid Unbalancing

 When bidding a construction contract it is important to consider the timing of progress payments as well as the amount of the bid itself. The progress payment schedule is directly related to the construction schedule since they are made based on the actual work completed, less some holdback (or retainage). In most cases, this results in the contractor incurring financing charges on the negative cash flow for most of the project duration. Progress payment therefore will have a significant impact on the amount of profit made. This is clear when the time value of money is considered and the present worth of the progress payment received is considered instead of just the cumulative sum of the payments.

One of the methods that the finance charges on the negative cash flow can be decreases, and thus increasing the profit, is by unbalancing the bid. A balanced bid is one where the actual costs and markups are accurately assigned to the appropriate bid items for unit price contracts. Unbalancing the bid means bidding the cost items that are completed earlier on in the project higher than the original marked up bid (i.e. balanced bid), while bidding the items that are completed later on in the project lower than the original balanced bid. This is done while maintaining the same total price unchanged. This is sometimes referred to as Front Loading the project.

Front loading is widely practiced on unit price contracts. In unit price contracts, the bidders usually provide a cost per unit for each line item on the bid form. The total bid amount is summed up and the contract is awarded based on the total combined bid. Unit price contracts are very common in heavy construction such as highway reconstruction and rehabilitation projects. Owners often use this type of contract when the exact scope and quantities of the work to be performed cannot be accurately determined. This shifts the risk to the contractor because of the inability to determine the exact quantities ahead of time, since the quantities on the bid forms are not always accurate. This is why most contracts include a renegotiation clause when the actual quantities differ significantly from those on the bid forms. A contract clause for example can read:

“Should the total as-built quantity of any major pay item required under the contract exceed the estimate contained in the proposal therefore by more than twenty five percent, the work in excess of the one hundred and twenty five percent will be paid for by adjusting the unit price… (Hinze, 2001)”

On the other hand, when the contractor knows from experience that there is a line item that a particular owner usually furnishes himself and therefore has a high probability of being eliminated from the contract, the contractor would deflate the cost of this line item and inflate a cost of another earlier on in the project. It is important to note therefore that the risk increases tremendously if the contractor decides to front load the project by unbalancing the bid, especially if the actual quantities differ from the quantities on the bid form within the limit specified in the contract and the contractor is not allowed to renegotiate the bid price. The contractor stands to loose a significant amount of money if he/she unbalances the bid and then it turns out that the quantities of those line items that he/she has inflated to front load the project, are actually less than the amount on the bid form.

Unbalancing can also occur on the schedule of values that the contractor is required to submit in lump sum bids. The owner uses to this schedule of values to determine progress payments to the contractor. The contractor would sometimes unbalance this schedule of values to front load the project. By unbalancing or front-loading the project, the contractor is in essence trying to get the majority of her/her money at the earliest possible time. The contractor might for example inflate the mobilization cost on the schedule of values and deflate the cost of another item later on in the project. In other words, the contractor is trying to increase the present worth of the payments from the owner. The present worth takes into account when the payment is made, by considering the time value of money. Therefore, the objective of bid unbalancing is to maximize the present worth of the payments by changing the bid prices for the different items within acceptable limits and at the same time keeping the bid price equal to that of the balanced bid (i.e. the bid before unbalancing). In the next section, the problem of maximizing the present worth of the progress payments is presented.

Problem Formulation

 Bid unbalancing have been addressed before in the literature (Ahuja and Campbell 1988, Stark and 1972). When there is a high degree of certainty regarding the quantities furnished by the owner in the bid form for a unit price contract or regarding the quantities and line items on a schedule of values, the bid unbalancing problem can be formulated and solved as a linear programming problem. Previous formulations of this problem, such as those in (Ostwald 2001, Taha 2001), consider maximizing the present worth of the progress payments received by the contractor. Mathematically this is expressed as:

When unbalancing the bid there are two constraints that should be addressed. Firstly, there is a constraint on the bid prices for the different line items themselves. Although most owners will accept unbalancing to some extent, the owner can disqualify a bid on the basis of obvious unbalancing [Hinze 2001]. The instructions to bidders in most contracts include a clause that “if the bid prices are obviously unbalanced, the owner has the option to reject the submitted bid….”. The contractor needs to establish reasonable upper and lower limits on his bid prices, so that the bid does not get rejected. This is expressed as:

In addition the present value of the progress payments cannot exceed the bid amount in order to maintain the competitiveness of the bid. This can be expressed as:

The linear programming problem formulated above can be solved manually using the simplex method. However, an easier approach would be to model and solve the problem using any commercial spreadsheet. In the next the proposed spreadsheet solution is presented.

Problem Solution

Spreadsheets provide a transparent way of modeling the problem, giving the user a complete understanding and control of the different variables and constraints in the problem. For the majority of construction problems, whose size usually ranges from small to medium, spreadsheet solutions are the most efficient and economical method to solve the problem. Excel provides a solver add-in, which can be used for optimizing such problems. In order to demonstrate the proposed spreadsheet model, consider the simple project shown in Figure 1. The problem presented here is adopted from (Ahuja and Campbell 1988). The project consists of 4 main activities. The main objective is to determine the unit prices to assign to each activity in order to maximize the present value. The proposed solution to this model involves a 4-step process.

Step One: Enter all the Required Data

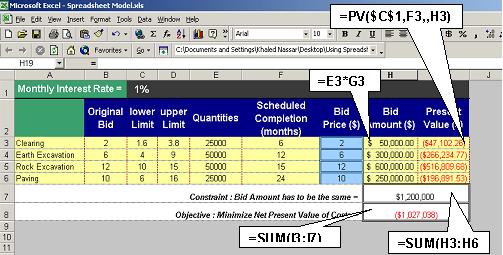
The first step is to enter all the required data into the spreadsheet. As shown in figure 2, the first and most important variable to consider it the monthly interest rate that will be used. Here, a contractor could use the interest rate that he/she expects to make on his/her money if the money was to sit in the bank. Secondly the upper and lower limits on the bid price have to be set. These values can be set from experience. Alternatively, a contractor could use the maximum fluctuation in the bid price before the bid can be disqualified as specified in the contract. The quantities and the scheduled completion values for the different activities can be determined from the actual project’s construction documents.

Table 1

The Example Project with Monthly Interest Rate at 1%

Step Two: Calculate the Present Value of the incomes

Once all the data has been entered the present value has to be calculated. In excel, the PV() function can be used to determine the present value of the progress payment for each of the activities in the project as shown in Figure 2. The present value function uses the bid amount (which is the quantity multiplied by the bid price), the scheduled completion time (or the time actual time that the payment is expected to be made), as well as the interest rate used. One can see that the proposed formulas are fairly straightforward and therefore can be easily utilized by contractors and understood by students. As formula (1) above suggests, the present value for the total project is simply the sum of all the present values of the different activities.

Step Three: Setup the solver variable, constrains, and objective

In order to solve this problem using the spreadsheet formulation we need to use the excel Solver Add-in. The Solver Add-in can be used to optimize a wide range of problems and is very robust and efficient in solving linear programming problems such as the one at hand. Therefore, the third step is to run the excel solver and maximize the present value of the progress payments. Figure 3 shows the parameters used in the model. The changing cells (or the problem variables) as well as the constraints as defined in the solver parameter dialog box. In addition to the traditional excel solver, there are a wide array of other commercial optimization add-ins available to handle larger problems. For example, the genetic algorithm solver add-in works with existing Excel Solver models to solve much larger problems up to hundreds of times faster.

Step Four: Run optimization and analyze the results

The last step is to run the solver add-in and generate the different solution reports. Table 3, shows solver answers report. Important information about the model can be extracted from this report. For example, it can be seen that by changing the bid prices from their initial balanced values (the “Original Value” column) to the new unbalanced values (the “Final Value” column), an increase of about $15,000 in the present value is possible ($1,041,963 – $1,027,038). This means that the contractor can make $15,000 more by the new cash flow. In order to achieve this increase in this simple example, once can see that the clearing and the earth excavation bid prices have been inflated to the their upper limit while a tradeoff in the rock excavation and paving bid prices has been reached. In addition, figure 4 shows how the interest rate affects the present worth of the payments. Expectedly, an increase in present worth can be achieved with a higher interest rate.

Table 3

Answer Report Generated by Solver

Conclusion and Recommendations for Future Research

This paper presented a useful application of spreadsheets to optimally unbalance the prices. By bidding the cost items that are completed earlier on in the project higher than the original marked up bid (i.e. balanced bid), while bidding the items that are completed later on in the project lower than the original balanced bid, the overall profitability of the project is increased. The optimum tradeoff between the bid prices was achieved using the developed spreadsheet model and the solver add-in. A number of future extensions are proposed for the developed model:  

References

 Ahuja, H., Campbell, W., (1988) “Estimating From Concept to Completion,” Prentice Hall Publishers, New Jersey

Stark, R. M., and R. L. Nicholas, (1972) “Mathematical Foundations for design: Civil Engineering systems,” McGraw Hill, New York

Philip Ostwald, (2001) “Construction Cost Estimating and Analysis,” Prentice Hall Publishers, New Jersey

Jimmie Hinze, (2001) “Construction Contracts,” McGraw Hill Publishers, New York

Hamdy Taha, (2001) “Introduction to Operation Research, Prentice Hall Publishers,” New Jersey

Christofferson, Jay P. (1999) “ Using Powerful Spreadsheet Application Tools to Increase the Efficiency and Effectiveness of Estimating”, ASC Proceedings of the 35th Annual Conference, California Polytechnic State University - San Luis Obispo, California, April 7 - 10, 1999, pp 197 –204

Christofferson, Jay P. (2000) “Estimating with Microsoft® Excel: Unlocking the Power for Home Builders”, BuilderBooks Publishers

Carmichael, J. (1997). 1997 Member Computer Study. Information Services Division, National Association of Home Builders