|
(pressing HOME will start a new search)
|
|
Symbolic Modeling in Engineering: A Complementary Course in Civil Engineering Curriculum
- John Kunz and Burcu Akinci
- Stanford University
- Stanford, California
Most of the courses taught in civil engineering departments of many universities focus on using numeric approaches to civil engineering and construction management problems. However, after graduation, construction managers often find themselves facing problems that are non-numeric (symbolic) in nature, e.g., safety analysis, generation of a construction plan, etc. There are formal approaches to model non-numeric problems using certain Artificial Intelligence techniques and object-oriented programming. The Civil and Environmental Engineering department at Stanford University offers a unique course, called Symbolic Modeling in Engineering, to complement the courses focused on numeric approaches. This course emphasizes the use of symbolic models to address civil engineering problems. Symbolic models represent and describe non-numeric aspects of engineering and incorporate formal qualitative reasoning mechanisms to make predictions, analyze and design an engineering phenomenon. First taught in 1989, the symbolic modeling course has helped to launch a number of successful Ph. D. theses and Masters' projects in which students have developed symbolic models of artifacts and processes as a principal research objective. This paper discusses the motivation for this unique course, the course objectives, and the course organization. It concludes with examples of Ph. D. studies that were initiated from this class, which apply symbolic modeling approaches to address civil engineering and construction management problems.
Key Words: Symbolic Modeling, Object-Oriented Programming, Artificial Intelligence, Qualitative Reasoning, Graduate Education
Introduction and Course Motivation
Engineering can be modeled in three ways: (1) Numeric modeling, e.g., uses the strength of a column for structural analysis, (2) Graphic modeling, e.g., uses lines, polygons and boxes to represent the shape of a column in three dimensions, and (3) Non-numeric (symbolic) modeling, e.g., uses words to describe the shape and the material of a column. Similarly, the engineering processes can be analyzed in two ways: (1) Quantitatively, e.g., structural analysis, fluid mechanics, etc., and (2) Qualitatively, e.g., algorithms, safety analysis, planning, etc. Most of the courses taught in civil engineering focus on the numeric aspects of the field, and approach civil engineering problems quantitatively. For example, the Civil and Environmental Engineering department at Stanford University offers three times as many classes that focus on qualitative aspects as the ones that focus on quantitative aspects of civil engineering (Stanford Bulletin 1998-1999).
In spite of this quantitative focus in the civil engineering curriculum, after graduation, young engineers often find themselves working on the non-numeric aspects of their jobs, such as safety analysis, project planning, and layout planning. This suggests that in addition to numeric models, it is important to have a formalized set of approaches to model and understand the symbolic aspects of our field. Artificial Intelligence techniques allow development of non-numeric (symbolic) tools to analyze engineering processes qualitatively. Consequently, the approaches developed in Artificial Intelligence together with object-oriented programming can be applied to non-numeric aspects of civil engineering and construction management.
In construction, we continuously deal with objects. Some of these objects are physical, such as columns, beams, and crew, and some of them are more abstract, such as construction activities (Figure 1). These objects have different attributes, namely numeric, non-numeric and relationship attributes. For example, a column has some numeric attributes, such as its length, width and height, as well as symbolic (non-numeric) attributes, such as its material. Similarly, an activity can have numeric attributes, such as its duration, early start and early finish dates, as well as symbolic attributes, such as predecessors, successors and crew type. There are three types of relationship attributes between different objects: (1) Numeric relationships, e.g., an increase in the quantity of resources assigned to an activity decreases the duration of an activity according to a numeric formula, (2) Non-numeric relationships, e.g., an activity precedes another activity, and (3) Hybrid relationships, e.g., Column 1 and Column 2 supports Beam 1 where the symbolic "support" relationship can be determined after quantitative structural analysis of the frame. As a result, to be able to adequately model a construction operation, it is important to define physical and abstract objects and their numeric, non-numeric and relationship attributes.
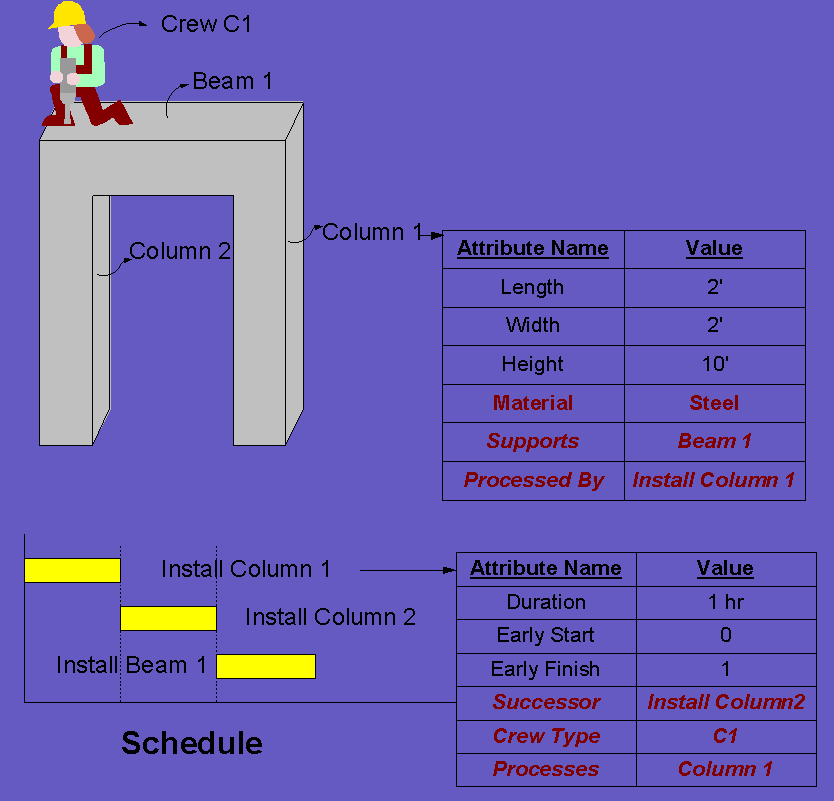
Figure 1. Example of physical and abstract objects used in construction and their numeric, symbolic and relationship attributes. Note that the symbolic attributes are written in bold and that the relationship attributes are italicized.
Currently, there is a trend in the construction management research area to use symbolic models and Artificial Intelligence techniques to formalize, describe and analyze complex engineering processes, devices and systems. Examples of the research projects that incorporate symbolic models to address construction management problems include the research done by Akinci and Fischer (1998), Aalami (1998), Thomsen (1998), Clayton et al. (1996), Christiansen (1994), Fruchter (1993), Cohen (1992) Froese (1992), Reddy (1992), Fischer (1991), Kunz (1991), Waugh (1990), and Darwiche et al. (1988). The Center for Integrated Facility Engineering (CIFE), an industry affiliates program of the Civil and Environmental Engineering and Computer Science departments at Stanford University, fosters research projects that apply symbolic modeling in addressing civil engineering and construction management problems. Some of these research projects developed at CIFE are successfully adapted by different companies in the construction industry. The final section of this paper discusses a sample of the CIFE research projects that apply symbolic modeling approaches to address challenging civil engineering tasks.
There is also an increasing trend among companies that provide technological support for the Architectural/Engineering/Construction (A/E/C) industry to model processes using symbolic modeling. The standardization efforts led by IAI (Industry Alliance for Interoperability) and STEP (Standard for the Exchange of Product Model Data) provide a library of standard definitions of A/E/C components, their attributes and relationships. As a result of these standardization efforts, there will be seamless data exchange and interoperability between different civil engineering and construction management software applications, such as computer aided design (CAD), cost estimating and scheduling software applications. Traditional CAD software applications represent building components graphically as lines and polygons, which are not useful for any engineering and construction management applications. With standardization, when an architect draws a column in a CAD software, it will be created as a column object for all the related applications, such as scheduling and cost estimating. Consequently, these applications will be able to utilize the necessary data related to that column to automatically generate a construction schedule and a cost estimate.
With this growing trend both in the industry and academia for modeling building components symbolically as objects and using these objects to automate construction engineering and management tasks, such as scheduling and cost estimating, construction managers need to have a good understanding of symbolic modeling approaches to take advantage of the next generation of software applications.
The next two sections describe the educational objectives of this class and the class organization. The last section provides examples of Ph. D. research studies launched from this class.
Course Objectives
The Symbolic Modeling in Engineering course is designed to achieve four objectives listed below. The class organization, which is composed of class discussions, readings, assignments, labs and term project, directly support these four objectives (Table 1).
Understanding the state of the art of symbolic model-based systems.
The course reader provides various symbolic modeling representation and reasoning examples from different fields, such as facility management , organizational modeling , assembly sequencing , construction planning , and construction information modeling . Additional examples are provided during class discussions. The class discussions, assignments and labs focus on both the basic engineering knowledge being represented and different approaches for symbolic representation and qualitative reasoning. Students are asked to discuss both organizational and technical factors, which determine the architecture of a symbolic modeling system. Moreover, they are encouraged to investigate specific alternative representations of entities (e.g., building components), relationships between entities, functional constraints of entities and behaviors of entities.
Relating models to business objectives and limits.
Class discussions and assignments emphasize formalization of business problems and the use of symbolic models to support business objectives. For the term project, student groups create a business plan to develop some technology, create and demonstrate a proof-of-concept prototype of their proposed development, and build an argument about how the business plan and demonstration complement each other.
Developing beginner skills in use of a symbolic modeling tool.
Through Lab demonstrations and hands-on programming tasks, the students learn basic representation, reasoning and user interface technologies. The objective is to learn to use computational modeling tools for developing symbolic models of products and processes. The class uses PowerModelÒ , a C-based object-oriented applications development shell, which runs on Sun computers under UNIX. This software is easy enough to be usable by students who have not been exposed to any object-oriented languages, such as C++ or Java. Consequently, students quickly develop basic programming skills to develop their own symbolic models for the term project.
Extending the thinking about engineering.
In an "hourglass" metaphor, engineering involves identifying and conceptualizing a problem (the top of hourglass), selecting and applying a solution method (the narrow passage), and applying results (the lower container of hourglass). The class focuses on all three aspects of the engineering. The students identify and conceptualize ill-structured problems, develop qualitative methods to analyze them, and then do testing and write proposals to interpret their results.
In addition to these four learning objectives, the symbolic modeling class emphasizes and enhances the improvement of broad intellectual process skills that all of us have, to some extent, but which all of us can improve. The class organization is designed to enhance the following five skills (Table 2):
Working effectively in teams.
Students work in small (2-3 person) teams for all assignments and the term project. The compositions of student teams change for each assignment to increase the learning from each student's experience. The term project involves both small and large-group collaboration depending on how students form their groups and define their project scope. Developing skills to work effectively in teams and learning from each team members' experience exponentially increase the learning curve of students.
|
|||||
Elements of the Course Organization |
|||||
Class Discussions |
Course Readings |
Assignments |
Term Project |
Labs |
|
| Understand symbolic modeling systems | ü |
ü |
ü |
ü |
ü |
| Relating models to business objectives | ü |
ü |
ü |
ü |
|
| Develop beginner skills in using a symbolic modeling tool | ü |
ü |
ü | ||
| Significantly extend thinking about engineering | ü |
ü |
ü |
ü |
|
| Table 2. The course organization is designed to enhance five intellectual skills of the students |
Elements of the Course Organization |
||||||
Class Discussions |
Course Readings |
Assignments |
Term Project |
Labs |
||
Educational Objectives |
Working effectively in teams | ü |
ü |
ü |
||
| Learning by doing | ü |
ü |
ü |
ü | ||
| Positive attitude about problem solving | ü |
ü |
||||
| Critical Thinking | ü |
ü |
ü |
|||
| Communicating effectively | ü |
ü |
ü |
|||
Learning by doing.
Modeling as an engineering practice can be learned only by doing it. The class emphasizes hands-on experience during class discussions and through assignments and term project.
Positive attitude about problem solving.
Engineering as a field involves both making and testing hypotheses. The class gives relatively formal theoretical background that can be used to create hypotheses about how things can be described, and it encourages testing student hypotheses with both quick mental experiments and using proof-of-concept computer demonstrations.
Critical thinking.
In engineering practice, and in symbolic modeling, cookbook solutions rarely can be used directly for interesting problems. We must modify existing approaches and design new solutions. We must exercise judgment in design and application of our solutions. The symbolic modeling course encourages the students to use their critical thinking in reading the course materials. The students are asked during class discussions and assignments to identify the purpose of the research projects described in the papers (including their assumptions and givens), and their representation and reasoning approaches.
Communicating effectively.
The course emphasizes clear and sharp oral and written communications. Classes are designed and executed as open discussion forums. Clear, sharp, concise, and responsive communication is required in written assignments.
Course Organization
The symbolic modeling is a 4-unit class offered in one quarter per academic year. It is open to all undergraduate and graduate students since symbolic modeling is applicable to all disciplines. The majority of the students are graduate civil engineering students focusing on construction management field. However, the class has always attracted students from a variety of backgrounds, such as, Mechanical Engineering, Engineering Economics Systems/Operations Research, Economics, Medical Informatics, Computer Science, and Industrial Engineering.
Class is organized around five elements:
Class discussions.
Three hours per week are allocated for class discussions. The students are expected to read the class material beforehand and actively participate in the class. The class follows an open format and promotes collaborative learning method. The instructor uses expert clusters approach , where participants form small groups to discuss an assigned topic and after discussing the groups report their findings to the large group, to enhance the students comprehension of the important topics. Group discussion approach is used when discussing the course readings and assignments. The discussions and questions are mostly directed back to the group. For example, all classroom participants address a question raised by a student, instead of the instructor providing an answer.
The instructor brings real engineering problems to the class and all of the students are expected to actively participate in discussion to define an approach to address that problem. An example of such a problem is the site layout problem where the goal is to develop a site layout that assigns the required space for trailers, crane, storage areas, access roads within the site, and that maximizes the adjacency requirements of these components. Students define the objects and attributes that are necessary to represent this problem and apply the configuration method discussed in the class to address this problem.
Course readings.
The course readings are designed around two goals: (1) To teach core symbolic modeling approaches and mechanisms , and (2) To discuss symbolic modeling samples from different domains .
Labs.
There are five laboratory sessions, one per week, for the first five weeks of the quarter. These labs provide hands-on experience with a symbolic modeling tool. The labs are designed so that each week's tutorial demonstrates a symbolic modeling reasoning and representation approach. Consequently, students experience the theoretical foundations in action. The labs also provide an environment where students get one-on-one response to their questions.
After the 5th week, the lab times are used for the development of the term project. The instructor and the teaching assistant continue to be present at the lab to address the students' questions as they arise while implementing their concepts.
Assignments.
There are assignments every week during the quarter. Three of the weekly assignments (Proof of Concept Technical Plan, Proof of Concept Summary and Proposal) are allocated for the term project. Students work in groups consisting of two students for each assignment. To promote learning from each other's experience, students are required to pair up with a different person for each assignment. All of the assignments submitted are posted on the web after the deadline, and students are encouraged to read other groups' assignments to understand and evaluate other groups' approaches.
The assignments promote clear and concise writing as well as responding to all of the questions being asked. It is expected from students that all written assignments have a professional content, organization and appearance without any grammatical and spelling flaws.
Term project and proposal.
The students team up consisting of 2-3 people per team to address an engineering problem of their interest using symbolic models. Project teams write a proposal for a symbolic model-based system and build a proof-of-concept demonstration in support of the proposal. The proposal is especially useful for students to match the purposes of their research to the purposes of their prototype model.
Many of the term projects developed in this class have formed the basis for many students' Ph. D. theses. Some of these Ph. D. theses are in turn commercialized in the construction industry. The section below discusses some of these Ph. D. research projects initiated from the Symbolic Modeling in Engineering course.
Ph. D. Research Projects Initiated from the Symbolic Modeling in Engineering Course
The approaches discussed in the Symbolic Modeling in Engineering course have influenced many Ph. D. students in formalizing their works. These Ph. D. works are grouped according to their fields:
Environmental Engineering. Perman (1989) has developed an expert system that assists an inexperienced waste water treatment plant operator in diagnosing and recommending remedial action for a limited number of operating problems.
Structural Engineering. Examples of the work done in this field include an emergency response system that determines the accessibility of the disaster areas , automation of conceptual design of structures in the preliminary structural design phase , and model-based reasoning for integrated structural design .
Architectural Design. Chinowsky (1991) developed a cooperative design tool with which designers can obtain assistance during the creation of space relationship diagrams.
Construction Engineering and Management. The Ph. D. work done in construction management field utilizing symbolic modeling approaches can be grouped into three areas: (a) Organizational Modeling, (b) Construction Plan Generation, and (c) Constructability Analysis
Organizational Modeling. Cohen (1992) developed the Virtual Design Team as an information-processing model of managerial decision-making. Later, Christiansen (1994) modified this model by developing a systematic method for describing the coordination load on different project team members, and with an explicit model of verification failures and decision making about how to handle the resulting work. Finally, Thomsen (1998) has introduced a new computational organizational model, called the Virtual Team Alliance, for investigating the effects of goal incongruency on the performance of semi-routine, fast-paced project organizations. These research projects done in organizational modeling using symbolic modeling approaches are commercialized with a tool called Vité-project (http://www.vite.com) to model, simulate, and analyze the predicted behavior of high-velocity, high-value strategic projects.
Construction Plan Generation. There have been a number of research projects focusing on generating a construction plan and schedule from intelligent design drawings, i.e. product models. One of the initial works in construction planning was done by Waugh (1990). He used a knowledge-based approach to represent a construction project and resources. Darwiche et al. (1988) defined a construction activity as composed of Objects (building components), Actions and Resources and developed a prototype tool that automatically generates construction plans from intelligent design drawings. Froese (1992) combined CAD product data, a plan generation expert system, an estimating program, and a scheduling application around a shared object-oriented database. Aalami (1998) developed a prototype system CMM (Construction Method Modeler), which uses method templates to generate a production model of a construction project. A company focused on technology development for the construction industry is currently working on commercializing CMM developed by Aalami (1998).
Constructability Analysis. There has been some research done to automate the constructability analysis using symbolic models. Fischer (1991) has developed an expert system that provides constructability feedback for reinforced concrete structures. Akinci (1998) is currently working on automating the identification of productivity and constructability problems due to spatial conflicts between concurrent activities.
Many of the Ph. D. students mentioned above are currently working in the universities and educating the next generation of construction managers and the construction management professors about the significance of symbolic modeling for the construction industry. Others are working in the private sector, and using the commercialized products, they are enhancing the efficiency and effectiveness of construction professionals and making them realize the capabilities of symbolic modeling.
Conclusion
The Symbolic Modeling in Engineering course complements the civil engineering curriculum by providing non-numeric modeling and qualitative reasoning approaches needed for addressing certain engineering problems. For the last ten years, the class has successfully educated students from various backgrounds about symbolic modeling. The symbolic modeling approaches taught in the class has helped several Ph. D. students to formalize their research approaches in addressing certain civil engineering problems. Previous graduates of the class are now impacting the construction industry by either applying symbolic modeling for the development of tools that enhance the efficiency and effectiveness of the construction professionals, or educating the next generation of construction managers about the capabilities of non-numeric modeling and qualitative reasoning.
References
Aalami F. (1998). Using Method Models to Generate 4D Production Models. Ph. D. dissertation submitted to Civil and Environmental Engineering department, Stanford University.
Akinci, B. & Fischer, M. (1998). Time-Space Conflict Analysis Based on 4D Production Models. Computing in Civil Engineering, Boston, ASCE, 342-353.
Basoz, N. (1996). Risk Assessment for Highway Transportation Systems. Ph. D. dissertation submitted to Civil and Environmental Engineering department, Stanford University
Bjork, B. (1992). A Unified Approach for Modeling Construction Information. Building and Environment 27,(2), 173-194.
Chinowsky, P. (1991). The CAADIE Project. Ph.D. dissertation submitted to Civil and Environmental Engineering department, Stanford University.
Christiansen, T. (1993). Modeling Efficiency and Effectiveness of Coordination in Engineering Design Teams. Ph.D. dissertation submitted to Civil and Environmental Engineering department, Stanford University.
Clayton, M., Kunz, J., & Fischer, M. (1996). Rapid conceptual design evaluation using a virtual product model. Engineering Applications of Artificial Intelligence, 1, (4), 439-451.
Cohen, G. (1992). The Virtual Design Team. Ph.D. dissertation submitted to Civil and Environmental Engineering department, Stanford University.
CTL (1997). Collaborative Learning Methods. Notes from CE 200, Teaching Assistant Class for Civil Engineering, a joint effort by Center for Teaching and Learning (CTL) and Department of Civil and Environmental Engineering, Stanford University.
Darwiche, A., Levitt, R. & Hayes-Roth, B. (1988). OARPLAN: Generating Project Plans by Reasoning about Objects, Action and Resources. AI/EDAM, 2, (3): 169-181.
Fischer, M. (1991). Using Knowledge During Preliminary Design of Reinforced Concrete Structures. Ph. D. dissertation submitted to Civil and Environmental Engineering department, Stanford University.
Froese, T. (1992). Integrated Computer-Aided Project Management Through Standard Object-Oriented Models. Ph. D. dissertation submitted to Civil and Environmental Engineering department, Stanford University.
Fruchter, R. (1993). Deriving alternative structural modifications based on Qualitative interpretation at the conceptual design stage. Proceedings of the 5th International Conference on Computing in Civil and Building Engineering, Anaheim, ASCE, 1243-1250.
Garcia, A. C. (1992). Active Design Documents. Ph. D. dissertation submitted to Civil and Environmental Engineering department, Stanford University.
Homem de Mello, L. S. & Sanderson, A. C. (1989). Representations of assembly sequences. 11th International Joint Conference on Artificial Intelligence, 56-61.
Jain, D. (1991). Logic-Based Conceptual Structural Design of Steel Office Buildings. Ph. D. dissertation submitted to Civil and Environmental Engineering department, Stanford University.
Kunz, J. (1989). Concurrent Systems Engineering. Working Paper #005, Center for Integrated Facility Engineering, Stanford University.
Kunz, J., Levitt, R., Lin, S. & Teicholz, P. (1995). The Intelligent Real-Time Maintenance Management (IRTMM) System: Support for Integrated Value-Based Maintenance Planning. Technical Report #100, Center for Integrated Facility Engineering, Stanford University.
Levitt, R., Christiansen, T., Cohen, G., Jin, Y. & Kunz, J. (1994). The Virtual Design Team: A Computational Simulation Model of Project Organizations. Working Paper #029, Center for Integrated Facility Engineering, Stanford University.
Luth, G. (1991). Representation and Reasoning for Integrated Structural Design. Ph.D. dissertation submitted to Civil and Environmental Engineering department, Stanford University..
Perman, C. (1989). Improving the Performance of Wastewater Treatment Plants. Ph. D. dissertation submitted to Civil and Environmental Engineering department, Stanford University.
Reddy R., Gupta, A., & Singh, R. (1992). Hueristic, symbolic logic and knowledge-based approach to the design and construction of buildings. Computers and Structures, 43, (6), 1191-1197.
Skolnick, J. (1993). A CAD-based construction simulation toolkit for construction planning. Proceedings of the 5th International Conference on Computing in Civil and Building Engineering, Anaheim, ASCE, 117,124.
Stefik, M. (1995). Introduction To Knowledge Systems, Morgan Kaufman.
Tendyke, R. & Kunz, J. (1989). Object-oriented programming. IBM Systems Journal, 28, (3), 465-478.
Thomsen, J. (1998). Virtual Team Alliance. Ph.D. dissertation submitted to Civil and Environmental Engineering department, Stanford University.
Waugh, L. M. (1990). A Construction Planner. Ph.D. dissertation submitted to Civil and Environmental Engineering department, Stanford University.
