|
(pressing HOME will start a new search)
|
|
Comparison of Construction Firms Based on Fuzzy Sets
- Amaury A. Caballero and Jack Dye
- Florida International University
- Miami, Florida
The paper builds upon and extends a previous work of the authors. It presents a methodology allowing individuals or organizations to compare the capacity of construction firms using a fuzzy logic expert system model. The paper briefly discusses the concept of fuzzy logic and the task of choosing an appropriate family of parametric membership functions by which to define capacity. The extended methodology is an alternative to a previously developed multiple attribute analytical hierarchical procedure that was developed to enable general contractors to rate the capacity of minority and small/disadvantaged business subcontractors. The model provides a means by which general contractors, private owners, or public agencies can rank competing construction organizations on matters other than the bid price for the work.
Key Words: Construction, Business Capacity, Fuzzy Logic
Introduction
General Contractors, private owners, and public agencies are often faced with a problem; how to evaluate the bids of competing construction organizations with respect to variables other than the lowest price. It is axiomatic that the each of these constituencies wants to choose from amongst the competing firms the one that best suits their needs. However, all too often the evaluation is made on the basis of cost alone with subsequent regret when the chosen firm proves incapable, for a variety of reasons, of performing the work (Barnes & Mitrani, 1991,1992).
The problem has been addressed in a previous work that led to the design of a multiple attribute analytical hierarchical expert system model (Ahmad & Dye, 1994). In order to use the model a list of attributes had to be developed and data accumulated for each firm that was under consideration. The list of attributes needed to be exhaustive but not so long as to be unwieldy. Additionally, the attributes should be independent of each other. A total of 18 attributes were used to demonstrate the model. Pair-wise comparisons were required in the definition of weighting functions, a step that requires the cooperation of the decision maker on the first round and in making any subsequent revisions.
Subsequently, the current authors proposed a modification to this expert system model through the incorporation of fuzzy logic (Caballero & Dye, 1998). Instead of pairwise comparisons that resulted in a specific point value, the fuzzy operators allowed a range of possibilities.
General Background
Borrowing directly from the authors’ previous work, fuzzy logic can be explained by the relative simple statements "I am hot" or "I am cold." In the first case, individuals generally do not say "I am 100 degrees," although if one did and if the listener carefully analyzed the statement, the meaning might be clear. More generally, the statement "I am hot" means that the individual is uncomfortable due to the ambient temperature, which might be somewhere between 80 and 100 degrees farenhieght. Similarly the statement, "I am cold," means that the ambient temperature is somewhere below, say, fifty degrees and that the individual is not dressed appropriately. This is the way that we speak and reason, and the use of such ranges with many different variables allows one to erect an expert system based on these ranges rather than on discreet points.
In a fuzzy system, each of the variables we need to describe a particularly situation or expert model can be described by a membership function. A membership function can be a linear relationship or a function that resembles a triangle, a normal distribution, or any other distribution that is reasonable for the attribute being described. As an example, going back to the "I am hot" statement, we can describe the membership function as follows:
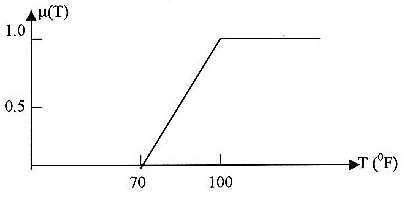
At any time an individual is experiencing an ambient temperature less than 70° F, the individual is not considered to be hot; Any individual experiencing an ambient temperature range between 70° F 100° F is considered to be some degree of hot; Any individual experiencing an ambient temperature over 100° F is considered to be hot.
This membership function derived is depicted in Figure 1, where the X axis represents the temperature (T), and the Y axis represents the degree of membership [m (T)].
Similar to utility values in utility theory, the membership function, m , varies between 0 and 1, and every one experiencing an ambient temperature of less than 70° F has a membership value of 0. Simply, those in cooler air are not hot and are not members of the hot group. Individuals experiencing an ambient temperature between 70° F and 100° F have a membership value varying linearly from 0 to 1, and those above 100° F have a membership value of 1.
Discussion
Extrapolation of fuzzy logic to an expert system requires that one follow the usual general outline:
Determination of the objective function. Exactly what is it that we are trying to do; Determination of the attributes that describe the essential features of the objective function; Determination of a means to rank these attributes with respect to each other; Collection of data; Analysis, results, and validation.
The latter two items are not discussed in this paper. In the present case, the desired
outcome is an expert system that allows individuals, agencies, or general contractors rank the capability of competing construction organizations to perform a certain project.
The second point of the general outline has been addressed by an extensive body of literature representing the opinions of various scholars on the common essential attributes of business organizations (Dye & Einstein, 1997). There is no intent by the authors to engage in that debate at this point. Instead, the attributes suggested in the earlier work by (Ahmad and Dye, 1994), reproduced here as Table 1, are stipulated as a sufficient starting point.
|
Figure 1. Example of a fuzzy set for the hot condition |
Table 1
Primary and Secondary Performance Criteria
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
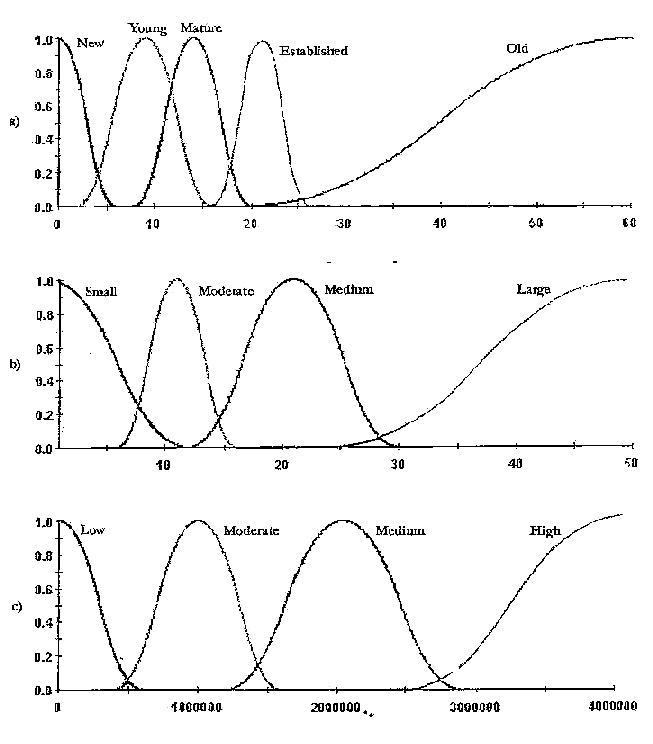
For the purposes of this and the original discussion, a single variable was chosen from each of the major groupings: number of full time personnel; number of years in business; and annual revenues. Figure 2 depicts nominal domains for these variables. The individual distributions were generated by software (Fuzzy Query 1.0) and no representation is made at this time that these are the actual distributions.
The descriptors of the particular attributes are as indicated on the individual figures. The actual descriptors need not be the same for different organizations using the model. All that is required is that the definition be understood and agreed to. Given that one of the essential features of fuzzy logic is that there are ranges of possibilities, the descriptors generally will have overlapping ranges.
It is instructive and central to the use of the fuzzy sets to consider how the sets can be used. If, for what ever reason, the preference is for a medium sized construction organization and the firm being evaluated has 22 full time employees, one would enter the horizontal scale at 22, move vertically until intersecting the "medium" distribution, and horizontally to the membership function. In the data depicted, the membership value, m , would be 0.8. If the number of full time personnel was less than 10 or more than thirty, then m would be 0. Similarly if the standard was anything other than medium, the membership function would also have been 0.
It is easy to see that organizations may fall within two (or more) distributions. The assumed fuzzy sets shown in Figure 2 can be used to demonstrate this fact. If one has an organization that has 9 full time employees it falls within both the small (m = 0.2) and moderate (m = 0.55) distributions. If the standard being evaluated is, say, moderate, then only the membership function for the moderate range is of interest.
If the variables are evenly weighted and none is more important than any of the others, a ranking may be established by computing the Compatibility Index (CI). The calculations will provide a rank ordering of the competitors and indicate how closely they are attuned to the specified standards. In this instance the CI is defined as the aggregate of all of the membership function values, m , divided by the total number of descriptors used (Cox, 1995). Logically, one has to ensure that the same descriptors and variables are used for all organizations and that the number of descriptors, N, is constant throughout the computations.
N
CI = [ S m i (x)]/N (1)
i=1
If it is considered that the different attributes are not of equal importance, then relative weights must be calculated. One simple method for determining such weights is the technique of successive comparisons. As an example, if a particular user of the model outlined above feels that P (personnel factors) should be 1.5 times as important as B (business experience factors), then the weights assigned would be 1.0 for B and 1.5 for P. Putting this aside, but considering that P is the most important factor thus far, the user would next rank P and F (financial). If the relative weight obtained as a result of this pairwise comparison is 2.0, then the relative weights for all three criteria will be:
B 1.0
P 1.5
F 1.5 x 2.0 = 3.0
Total 5.5
If these are normalized the resulting weights are as follow:
BUSINESS EXPERIENCE : 1.0/(1.0 +1.5+3.0) = 0.182
PERSONNEL: 1.5/(1.0 +1.5+3.0) = 0.273
FINANCIAL: 3.0/(1.0 +1.5+3.0) = 0.545
Having the relative weights, the modified formula for the compatibility index calculation becomes:
N
CI = S w i m i(x) (2)
i=1
where w i is the weight of attribute and the other terms are as defined in equation (1).
The weighting of attributes may change the rank ordering of the CI for construction organizations when compared to the calculations where no weighting is utilized. To the extent that this is true, then the model more clearly reflects the concerns of the ranking organization. If an examination of the CIs, computed using weighted and non-weighted attributes indicates that there is no change in the ranking, or that the differences in the relative differential between the CIs computed by either method is small, then the weighting refinement may be unwarranted. The trivial case is, obviously, when all of the weights are approximately equal.
As a demonstration of the utility of the use of fuzzy logic in the selection of construction organizations using other than cost factors, the authors designed 6 hypothetical firms as indicated in Table 2. Only the three attributes shown in Figure 2 were utilized.
Table 2.
Firms and Attributes
Firm |
Full time employees |
Annual revenues (millions of $) |
Business experience (years) |
A |
10 |
5 |
5 |
B |
23 |
12 |
14 |
C |
30 |
25 |
10 |
D |
37 |
31 |
16 |
E |
16 |
27 |
8 |
F |
25 |
18 |
6 |
The unweighted calculations for the Capability Index were performed utilizing the same software that generated the fuzzy sets. The weighted calculations were done manually. The results of both are displayed in Table 3.
Table 3.
Fuzzy Set Calculations
Firm |
Equation (1) |
Equation (1) rank |
Equation (2) |
Equation (2) rank |
A |
0.018 |
4 |
0.054 |
4 |
B |
0.563 |
1 |
0.763 |
1 |
C |
0 |
0 |
||
D |
0 |
0 |
||
E |
0.128 |
3 |
0.055 |
3 |
F |
0.206 |
2 |
0.327 |
2 |
|
Figure 2. Fuzzy Sets: a) Business Experience b) Number of Employees c) Annual revenues |
Two things are immediately apparent: for the sample calculations, there was no change in the ranking between the weighted and unweighted data despite the fact that one variable was considered three times as important as another; and firms A and E declined markedly as a competitors when compared to the two leading firms. Additionally, Firm B is more compatible with the assumed requirements under the weighted system, showing that it closely conforms to the stated conditions.
Conclusions
The extension of the model previously presented provides a refinement that allows the user of the basic model to more completely reflect their concerns in the ranking of competing firms. Quoting from the original work, "The power of the fuzzy logic model is that it uses imprecise terms to arrive at ‘crisp’ values." Modifying these ‘crisp’ values by establishing weights, reflecting the importance of various attributes, is a logical next step.
The use of software to both generate the fuzzy sets and perform calculations provides the necessary link between theory and practice. The number of manual calculations that would be required to examine several competitors and more than a small number of attributes is excessive, time consuming, and would surely discourage any practical application of the work.
An additional effort is required to demonstrate the usefulness of the model. In particular, it is necessary to move to the practitioners to:
| Develop the attributes that are of concern; | |
| Develop the distributions for the descriptors | |
| Develop the weights and see if these can be generalized throughout the construction industry. |
References
Ahmad, I., & Dye, J. M. (1994). Development of a Database of MBE/DBE Firms and Decision Model to Determine Their Capacity for the Florida Construction Industry. Miami, FL: Technical Report 120, Department of Construction Management, Florida International University.
Barnes, W. C. & Mitrani, J. D. (1991). Develop and Teach a Course on Practices and Pitfalls in the Construction Industry that are Subject to Law Suits. Miami, FL: Technical Report 102, Department of Construction Management, Florida International University.
Barnes, W. C., & Mitrani, J. D. (editors) (1992). Practices in the Construction Industry Which are Subject to Law Suits. Miami, FL: Technical Report 108, Department of Construction Management, Florida International University.
Caballero, A. A., & Dye, J. M. (1998). Application of a Fuzzy Logic Model to Compare the Capacity of Construction Firms. Proceedings of the Associated Schools of Construction Southeast Regional Meeting. Atlanta, GA.
Cox, E. D. (1995). Fuzzy Logic for Business and Industry. Charles River Media, Inc., Rockland, Massachusetts.
Dye, J. M., & Einstein, W. A. (1997). A History of Efficiency & Effectiveness: With an Introduction to n Space. The Journal of Applied Management and Entrepreneurship, 3, No. 1, pp 99+.
Fuzzy Query 1.0. (1998). Sonalysts, Inc., 215 Parkway North, Waterford, CT. 06385
Goodwin, P., & Wright, G. (1998). Decision Analysis for Management Judgement, 2nd edition. John Wiley & Sons, West Sussex, England.